Know About Quadratic Equation: 4x ^ 2 – 5x – 12=0

by
Know About Quadratic Equation: 4x ^ 2 - 5x - 12=0

Mathematics contains many quadratic and algebraic equations, and 4x^2 – 5x – 12=0 is an example. The following article will guide you through solving this quadratic equation. While it may seem complex at first, as it requires finding the value of x, you will find and it is quite simple once you begin the process.

Continue reading the article below for detailed steps on how to solve it. Please see below:

Know what are quadratic equations?

Quadratic equations are a fundamental topic in mathematics. Let’s explore them:

Quadratic equations, also known as quadratics, are polynomial equations of the second degree. This means they contain at least one term that is squared.

The general form of a quadratic equation is: ax2+bx+c=0

Here, (x) represents an unknown variable, and (a), (b), and (c) are numerical coefficients.

For example, (x^2 + 2x + 1) is a quadratic equation, where (a \neq 0). If (a) were equal to zero, the equation would become linear (not quadratic).

Roots or Zeros:

The solutions to a quadratic equation are the values of the unknown variable (x) that satisfy the equation.

These solutions are called roots or zeros of the quadratic equation.

Standard Form:

The standard form of a quadratic equation is: ax2+bx+c=0. It is univariate (contains only one unknown variable) and has the highest power of (x) as 2.

Quadratic Formula:

To find the roots of a quadratic equation, we use the quadratic formula:

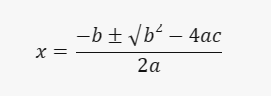
Examples:

Quadratic equations:

  • (x^2 – x – 9 = 0)
  • (5x^2 – 2x – 6 = 0)
  • (3x^2 + 4x + 8 = 0)

Quadratic equations without a constant term (c):

  • (-x^2 – 9x = 0)
  • (x^2 + 2x = 0)
  • (-6x^2 – 3x = 0)

Factoring, Completing the Square, and the Quadratic Formula:

There are different methods to solve quadratic equations:

  • Factorization: Find what to multiply to obtain the quadratic equation.
  • Completing the Square: Transform the equation into a perfect square trinomial.
  • Quadratic Formula: Use the formula to directly calculate the roots.

Related Articles

Characteristics of the 4x ^ 2 – 5x – 12=0 quadratic equation

4×2−5x−12=0 has several characteristics that define its graph and solutions:

Parabolic Shape: The graph of this equation is a parabola, which is a symmetric curve with a single peak or trough.

Vertex: The vertex of the parabola is the point that represents the maximum or minimum value of the quadratic function. For the given equation, the vertex can be found using the formula

x=-b/2a,

which gives the x-coordinate of the vertex. In this case, the vertex is at x=5/8​ , and by plugging this value into the equation, we find the y-coordinate of the vertex to be approximately

y=−13.5625 .

Axis of Symmetry: The line of symmetry of the parabola passes through the vertex and divides the parabola into two mirror-image halves. For this equation, the axis of symmetry is the vertical line

x=5/8.​

Roots: The roots (or x-intercepts) of the quadratic equation are the values of x for which the equation equals zero. This equation has two distinct real roots, which can be found using the quadratic formula:

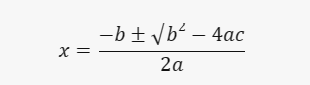
Substituting the values of a, b, and c from the equation, we get the roots as approximately x=−1.216 and x=2.466.

Discriminant: The discriminant of a quadratic equation, given by b2−4ac , determines the nature of the roots. A positive discriminant indicates two distinct real roots, which is the case for this equation with a discriminant of 217.

These characteristics help us understand the behavior of the quadratic function and its graph, which can be useful in various applications such as physics and engineering.

How to solve 4x ^ 2 – 5x – 12=0

There are two main methods:

Factoring Method

This method involves finding two binomials that, when multiplied together, give the original quadratic equation. The solution is found by setting each binomial equal to zero and solving for x, resulting in x = -3/2 and x = 2.

Quadratic Formula

The quadratic formula

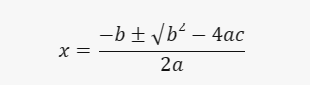
  • (the above formula) is used, where a, b, and c are coefficients from the equation. By substituting the values into the formula, the solutions for x are again x = -3/2 and x = 2.

These methods are explained as simple and effective, suitable for students to solve quadratic equations.

Conclusion

The article explains that it has covered two main techniques for resolving the quadratic equation

4×2−5x−12=0. It suggests that readers can refer to these methods within the article to effortlessly tackle this particular quadratic equation. Additionally, it highlights the ease of use of these methods, making them accessible to students of all levels.